人工智能框架峰会 | MindSpore Quantum量子计算化学研究工具，助力量子化学科研百倍效率提升

　　据悉，昇思MindSpore开源社区将于 2025 年 12 月 25日在杭州举办昇思人工智能框架峰会。本次大会的AI for Science创新论坛策划，将会分享基于昇思MindSpore的在AI科学计算领域的前沿成果，欢迎现场交流。本文介绍MindSpore Quantum在量子化学领域的效率提升。

　　在量子化学模拟中，随着系统规模扩大，希尔伯特空间维度的指数级增长给经典验证带来了算力瓶颈。针对这一问题，MindSpore Quantum 推出了 mqchem 模拟器。该模块利用化学体系中的粒子数守恒定律，将计算限制在有效的量子态子空间内，从而在经典硬件上显著减少了模拟所需的内存与时间，为开发和验证复杂分子的量子算法提供了高效的工具。

　　量子化学研究领域的挑战

　　量子计算的最初灵感，来源于物理学家理查德·费曼（Richard Feynman）对微观世界模拟的深刻洞察：“自然不是经典的，如果你想模拟自然，你最好让它成为量子力学的。”

　　在药物设计、催化剂研发等领域，核心任务是求解多电子体系的薛定谔方程。理论上，量子计算机能够利用量子比特的叠加与纠缠特性，天然地模拟微观粒子的强关联作用。但在当前的含噪声中等规模量子（NISQ）时代，量子硬件资源依然稀缺且充满噪声。因此，在经典计算机上构建高性能的量子模拟器，成为开发和验证量子算法不可或缺的环节。

　　然而，经典模拟器面临着巨大的挑战。随着电子数量增加，描述系统所需的希尔伯特空间维度呈指数级爆炸式增长，这被称为“维数灾难”。为了在有限的经典算力上验证未来的量子算法，MindSpore Quantum 推出了专注于化学场景的 mqchem 模拟器。它旨在通过软件算法层面的优化，让开发者能够在经典硬件上更高效地运行如 变分量子本征求解器（VQE） 等前沿算法。

　　对于熟悉AI的开发者，VQE可以被理解为一个量子版本的神经网络训练过程：

　　• 模型构建：参数化的量子线路（Ansatz）类比于神经网络模型；

　　• 目标函数：分子的基态能量期望值类比于Loss函数；

　　• 优化迭代：通过经典优化器更新线路参数，直至能量收敛。

　　核心技术：利用物理守恒量加速经典模拟

　　通用的全振幅量子模拟器为了模拟任意量子系统，通常基于2^n维的全空间构建。这种“通用性”在模拟特定化学问题时，变成了巨大的算力负担。因为在非相对论量子化学中，分子体系遵循粒子数守恒定律——无论电子如何在轨道间跃迁，电子的总数量是恒定的。这意味着，在全空间的经典模拟中，绝大多数计算资源被浪费在了物理上无效的状态上。为了解决这一计算资源冗余的问题，MindSpore Quantum 的 mqchem 模拟器利用粒子数守恒的物理特性，不再构建全希尔伯特空间，而是将模拟限制在有效的量子态子空间（即组态相互作用空间）内。通过这种方式，mqchem 模拟器避免了对物理上无效状态的存储与运算，从而能够更高效地在经典计算机上处理化学模拟任务。

　　让我们以一个拥有 20个自旋轨道 且填充了 10个电子 的分子体系为例，对比通用模拟器与 mqchem模拟器的区别：

　　• 通用模拟器（全空间）：必须开辟2^n（约105万）维的内存空间。它机械地处理从|00...> 到 |11...1>的所有状态，哪怕其中包含大量“3个电子”或“15个电子”这种在化学反应中不可能出现的无效态。

　　• mqchem 模拟器（CI子空间）：利用物理先验知识，采用组态相互作用（Configuration Interaction, CI）基，仅构建和存储电子总数守恒的量子态。此时，需模拟的空间维度缩减为C(20,10)（约18万）。

　　通过这种基于物理守恒的优化，模拟所需的向量维度直接降低了约82%。

　　需要强调的是，这种优化是针对经典模拟器的加速策略（真实的量子计算机不需要这种优化，因为它天然并行）。mqchem 模拟器在底层针对这种紧凑向量表示实现了专用的算子适配（如 UCCExcitationGate）。由于避免了对无效状态的冗余计算，且向量长度显著缩短，线性代数运算效率得到了质的飞跃。这使得我们能够在没有大规模容错量子计算机的当下，利用现有的经典资源，去探索和验证更大规模、更深线路的分子模拟算法。

　　应用范例：进阶VQE算法的高效构建与求解

　　为了体现MindSpore Quantum在处理复杂量子化学算法时的通用性与高效性，我们基于 mqchem 模拟器实现了三种改进版本的 VQE 算法：Sym-UCCSD、ADAPT-VQE 和 k-UpCCGSD。

　　A. Sym-UCCSD

　　针对 UCCSD 拟设存在量子线路深度过大的问题，Sym-UCCSD (symmetry-reduced unitary coupled-cluster singles and doubles) 方法 [1] 以分子点群对称性为核心约束，通过筛除不满足分子点群对称性要求的激发算符，构建出更精简的拟设形式。

　　该方法的具体实现流程如下：

　　• 基于分子的几何结构，确定其所属的点群；

　　• 推导各分子轨道对应的不可约表示，并构建相应的不可约表示乘积表；

　　• 根据涉及的分子轨道，明确参考态的不可约表示；

　　• 计算各激发算符作用后生成的激发态的不可约表示；

　　• 滤除拟设中所有对应激发态不可约表示与参考态不可约表示不同的激发算符。

　　MindSpore Quantum 提供了灵活的线路构建接口与 mqchem 模拟后端，支持开发者快速实现基于对称性的算符筛选，并高效评估精简后的拟设在能量计算上的表现。

　　这里，我们基于 pyscf 开发包自动化实现上述步骤，并使用 mqchem 模拟器执行构造出的拟设，计算氟化氢（HF）分子的基态能。

　　为简洁起见，我们将部分代码封装成了函数。完整代码已托管到 MindSpore Quantum 仓库，感兴趣的读者可以从此链接获取。

　　（https://gitee.com/mindspore/mindquantum/tree/master/example/advanced_vqe）

　　输出结果显示，引入对称性约束后，Sym-UCCSD 的参数量由 20 降至 11，激发算符数量由 35 降至 17。同时，两种拟设的计算误差均维持在10^-7量级，表明精简后的模型在降低复杂度的同时保持了计算精度。

　　我们还对比了该任务在通用模拟器与 mqchem 模拟器上的执行时间。

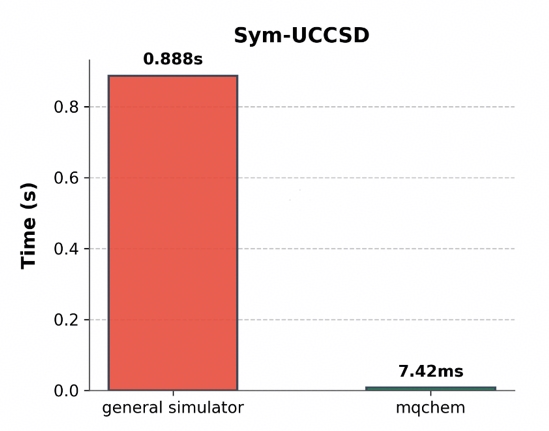
　　如上图所示，通用模拟器耗时约 0.888s，而 mqchem 模拟器耗时为 7.42ms。由于 mqchem 模拟器仅在粒子数守恒的子空间内进行矩阵运算，不仅降低了维度，也显著减少了模拟所需的时间。

　　B. k-UpCCGSD

　　传统 UCCSD 拟设的激发算符数量随分子轨道数 N 呈O(N^4)规模增长，即便采用最大并行执行策略，其量子线路深度仍维持在O(N^3) 级别，这一高复杂度限制了其在中大分子体系中的实际应用。为突破这一瓶颈，Joonho Lee 等人提出了 k-UpCCGSD (k-Unitary Pair Coupled-Cluster with Generalized Singles and Doubles) 拟设方案 [2]，实现了拟设复杂度的显著降低。

　　k-UpCCGSD 拟设的核心激发算符集合包含两类关键成分：

　　• 所有广义单激发算符（generalized single excitation operators）；

　　• 所有 “成对的” 广义双激发算符（paired generalized double excitation operators）。

　　其中，“广义”指的激发算符的作用范围不受限于传统 UCCSD 中占据轨道到虚拟轨道（occupied → virtual）的跃迁模式，而是进一步涵盖占据轨道间（occupied → occupied），以及虚拟轨道间（virtual → virtual）的跃迁过程，从而更全面地捕捉电子关联效应；“成对的” 双激发算符则是将跃迁过程约束于两个分子轨道对之间，从而降低双激发算符的数量。为进一步提升能量计算精度，可将上述基础拟设单元重复堆叠 k 次，且每次堆叠所对应的参数相互独立，形成 k 层拟设结构。

　　k-UpCCGSD 拟设的激发算符数量仅随 N呈O(N^2)增长，结合并行执行策略后，量子线路深度可优化至O(KN)，也即实现了线性级别的线路深度。

　　MindSpore Quantum 内置了对广义激发算符的支持，结合 mqchem 模拟器对梯度的加速计算，使得在经典计算机上评估此类深层参数化线路成为可能。为直观展示 K-UpCCGSD 拟设的构造逻辑，本节以氟化氢分子基态能量求解作为案例，并基于 mqchem 模拟器完成拟设的仿真计算。

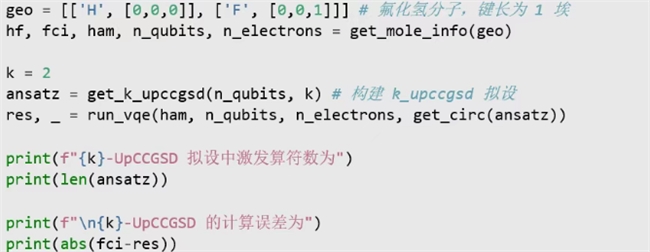
　　实验结果表明，2-UpCCGSD 拟设共包含 90 个激发算符，其计算能量与 FCI 理论值的误差仅为1.8 ×10^-12Ha，显示出该拟设在处理电子关联效应上的准确性。

　　性能对比

　　在变分算法中，参数梯度的计算效率直接影响训练速度。下图展示了单步梯度计算的时间开销。通用模拟器耗时 65.60ms，而 mqchem 模拟器耗时 0.54ms。这种在梯度计算上的性能优势，有助于加快多层拟设的参数优化过程。

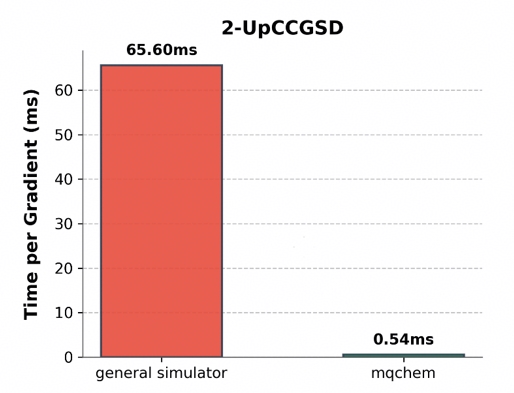
　　C. ADAPT-VQE

　　与前述 Sym-UCCSD、k-UpCCGSD 两类固定结构的量子拟设不同，ADAPT-VQE（Adaptive Derivative-Assembled Pseudo-Trotter ansatz Variational Quantum Eigensolver） 算法 [3] 采用动态构建拟设的核心思路：首先将 UCCSD 拟设包含的所有激发算符整合为一个完备的“激发算符池”，通过迭代优化机制逐步筛选关键激发算符，最终形成适配目标分子体系的精简拟设。

　　其具体迭代流程如下：

　　1、初始化空拟设与参考态，设定梯度阈值等终止条件；

　　2、在每次迭代中，计算激发算符池中所有激发算符在当前拟设态、参数为 0 时的能量梯度；3、选取梯度绝对值最大的激发算符（即对能量降低贡献最显著的算符）加入拟设；

　　4、优化当前拟设的所有参数直至收敛，随后进入下一轮迭代；

　　5、若某轮迭代中，算符池内所有剩余激发算符的梯度向量范数小于预设阈值，则终止迭代。

　　ADAPT-VQE 具备显著的方法优势：首先，该方法可以自动挑选出最关键的激发算符构造紧凑的拟设，线路深度浅；其次，通过调整梯度阈值等终止条件，原则上可逼近任意精度要求；最后，采用“暖启动”优化策略，新增激发算符后直接复用前序迭代的最优参数，不仅提升了收敛效率，还能有效缓解量子优化中常见的局部最优问题与贫瘠高原现象。

　　ADAPT-VQE 算法需要在每次迭代中评估算符池内大量算符的梯度。mqchem 模拟器的高效模拟能力可以显著缩短这一筛选过程的计算时间，提升算法整体的运行效率。

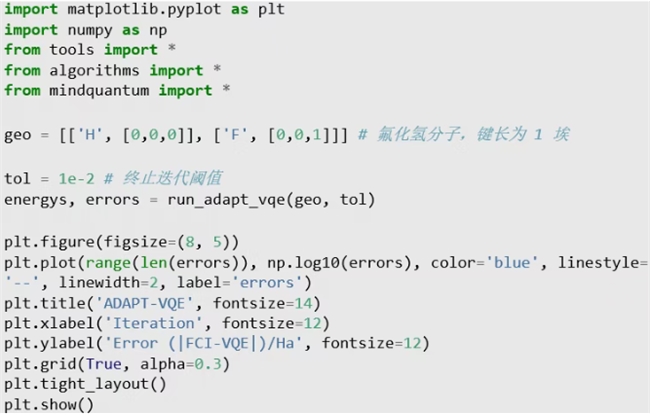
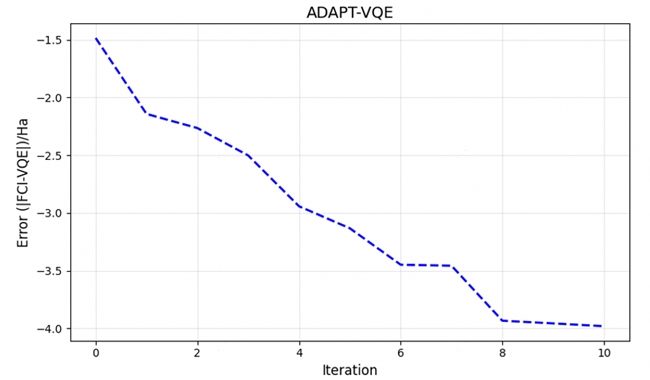
　　以上收敛曲线展示了优化过程：随着关键算符被逐步选入拟设，能量误差在对数坐标下呈近似线性下降，并最终达到预设精度。

　　我们还对比了 ADAPT-VQE 算法在算符筛选与优化阶段的耗时情况。

　　如上图所示，通用模拟器耗时 0.945s，而 mqchem 模拟器耗时 5.47ms。在处理需要频繁进行梯度评估的自适应算法时，mqchem 模拟器能够有效减少计算资源的消耗。

　　MindSpore Quantum是基于昇思MindSpore开源深度学习平台开发的新一代通用量子计算框架，聚焦于NISQ阶段的算法实现与落地。结合HiQ高性能量子计算模拟器和昇思MindSpore并行自动微分能力，MindSpore Quantum有着极简的开发模式和极致的性能体验，能够高效处理量子机器学习、量子化学模拟和量子组合优化等问题，为广大科研人员、老师和学生提供快速设计和验证量子算法的高效平台，让量子计算触手可及。

　　MindSpore Quantum开源仓库：

　　https://atomgit.com/mindspore/mindquantum

　　MindSpore Quantum社区文档地址：

　　https://www.mindspore.cn/mindquantum/docs/zh-CN/r0.11/index.html

　　[1] Cao C, Hu J, Zhang W, et al. Progress toward larger molecular simulation on a quantum computer: Simulating a system with up to 28 qubits accelerated by point-group symmetry[J]. Physical Review A, 2022, 105(6): 062452.

　　[2] Lee J, Huggins W J, Head-Gordon M, et al. Generalized unitary coupled cluster wave functions for quantum computation[J]. Journal of chemical theory and computation, 2018, 15(1): 311-324.

　　[3] Grimsley H R, Economou S E, Barnes E, et al. An adaptive variational algorithm for exact molecular simulations on a quantum computer[J]. Nature communications, 2019, 10(1): 3007.

　　本次在杭州举办的昇思人工智能框架峰会，将会邀请思想领袖、专家学者、企业领军人物及明星开发者等产学研用代表，共探技术发展趋势、分享创新成果与实践经验。欢迎各界精英共赴前沿之约，携手打造开放、协同、可持续的人工智能框架新生态！